VOL 3, ISSUE 2
Z-Value Calculation
By Boden Larson, IT Manager
What is a Z-value?
A Z-value is defined as the number of degrees (Celsius or Fahrenheit) required to change a D-value by one factor of ten. In the practical sense, it is a measure of how susceptible a spore population is to changes in temperature. For example, if the Z-value of a population is 10 degrees, then increasing the sterilization temperature 10 degrees will result in a log reduction of the D-value.
The Z-value can be found by plotting D-values against temperatures on a semilogarithmic scale and adding a line that best fits the data. The absolute value of the reciprocal of the slope of this line will be the Z-value.
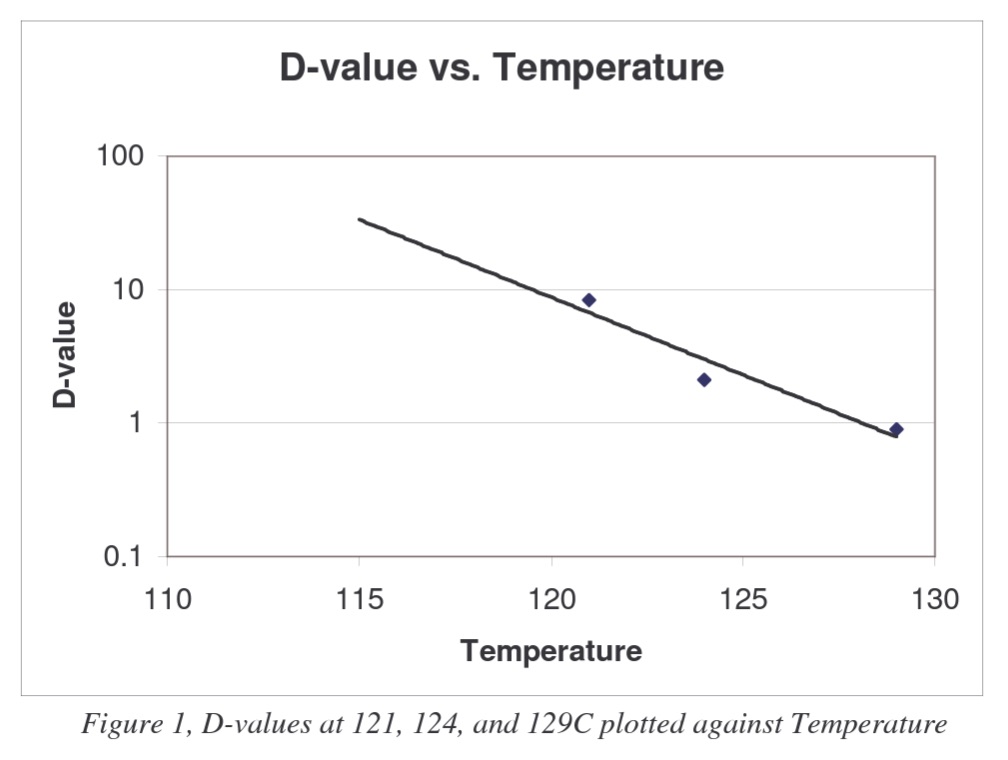
Since D-values are plotted logarithmically, the line of best fit will be of exponential form and will therefore appear linear on semi-logarithmic paper, as shown above in Figure 1.
Why use a line-of-best-fit?
In a perfect world, the D-value of a particular spore will decrease exponentially as temperature is increased. In reality however, D-values will not decrease perfectly due to natural variations and experimental error. A line-of-best-fit is a statistically correct method of representing the data points.
How do I determine a Z-value graphically?
Calculating a Z-value graphically is relatively easy. Plot at least 3 D-value/temperature pairs on a semi-logarithmic graph and, using your best judgement, draw a straight line through the points that most closely fits the data. From this line, determine the number of degrees required to change the D-value by one factor of 10 (see Figure 2 below).

In the above case the Z-value appears to be approximately 8°C.
Can I determine a Z-value mathematically?
Yes. Estimating a Z-value graphically is far less perfect than calculating a Z-value mathematically.
To accomplish this we must know the equation for our line-of-best-fit, or more specifically the slope of our line, which can be found using a log-linear regression analysis.
The following normal equations can be used to find the equation of a linear regression line:
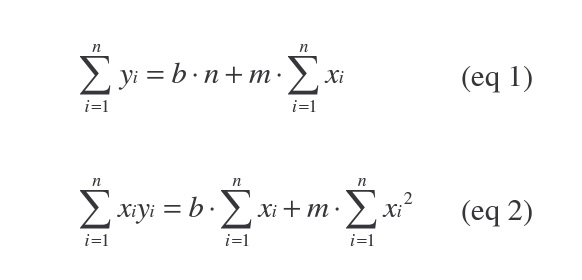
where:
- b is the y-intercept of the regression line
- m is the slope and
- n is the number of x, y points.
Since, however, we are dealing with x, log y pairs, the above equations must be modified to reflect our log-linear scale:
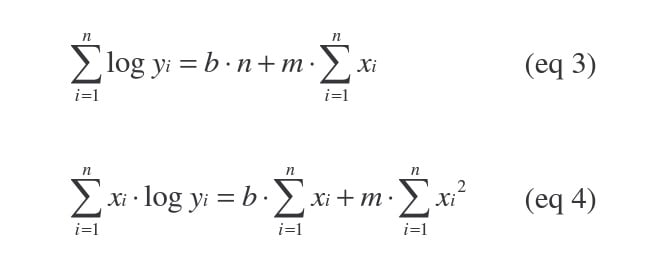
Now, using the method of least squares, we can find the following formula for the slope of our line:
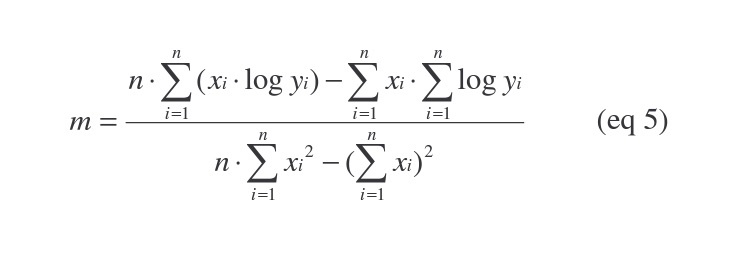
where
- n is the number of D-value/temperature pairs (data points)
- x represents temperature and
- y represents D-value
From this equation we can find the Z-value by taking the absolute value of the reciprocal of this slope, as such:
Z = |1/m| (eq 6)
Why is the Z-value the reciprocal of the slope? Explain further.
Take another look at Figure 2. As you can see, the slope ("rise over run") of our regression line is:
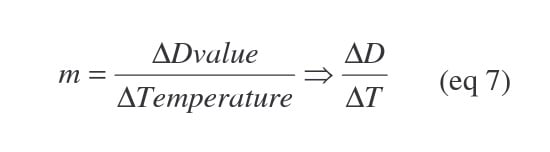
By the definition of a Z-value, we are only concerned with a 1 log reduction in the D-value. Therefore we fix our change in D-value (∆D) at1.
m = 1/∆T (eq 8)
In so doing, this change in temperature now becomes our Z-value.
m = 1/Z (eq 9)
And solving for Z gives us:
Z = 1/m (eq 10)
Finally, since the Z-value should always be a positive value (and slope of our regression line can be negative), we take the absolute value of our equation:
Z = |1/m| (eq 11)
Example 1:
Calculate a Z-value from the following D-values:
Temperature, D-value
- 115°C, 8.9 minutes
- 121°C, 2.1 minutes
- 124°C, 0.9 minutes
Construct a table to simplify the calculation:

number of x, y pairs = n = 3
Now plug these values into the equation for the slope of our regression line (eq 5).
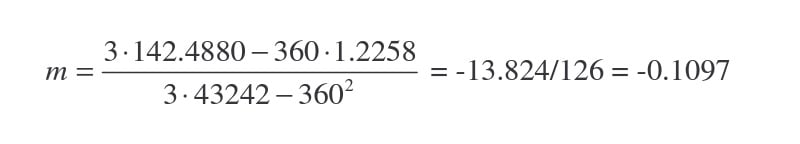
Now solve for Z (eq 6).
Z = |1/-0.1097| = 9.1
Ok, I understand Z-values. How do I determine a D-value from a Z-value and known D-values?
While this task is self-explanatory when done graphically, it is rather difficult to perform mathematically.
First we must define the problem. If we have, say, three D-value/temperature pairs, then we are looking for a fourth D-value at a given temperature. Therefore we are solving for an unknown D at a specified temperature. The unknown D-value should fit our regression line in such a way as not to affect its slope, thereby not changing the Z-value.
Performing this task will require that we know the entire data set that was used to generate the Z-value specified. While all of this data may not be included on a certificate of performance, it can in most cases be obtained by contacting Mesa Laboratories.
We must expand our original equation for the slope of a log-linear regression line to include the unknown D-value.
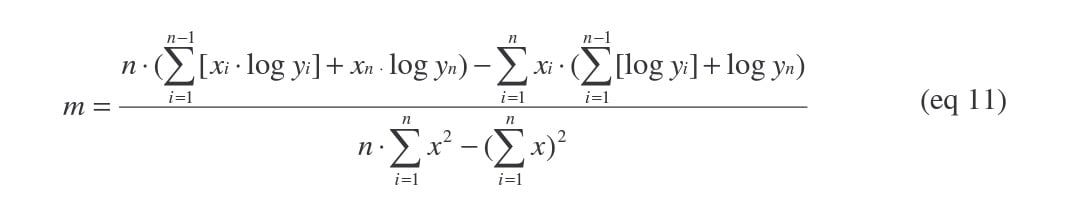
Since the Z-value is known, we can substitute for m:
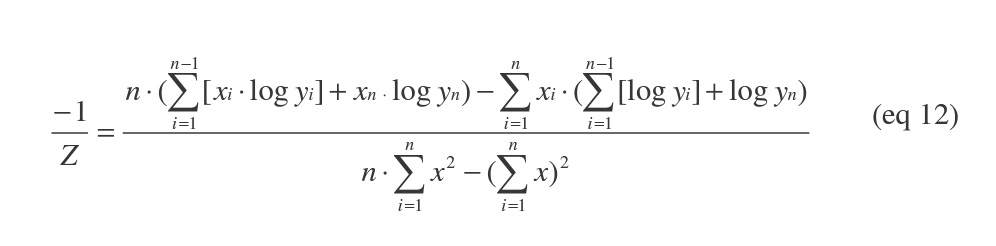
Note that we've substituted -1/Z for m instead of the absolute value of 1/Z. This is due to the fact that our D-values are assumed to decrease as temperature increases, thereby causing the slope of our regression line to be negative. If the D-value was to increase with temperature then we would use 1/Z, however it is highly unlikely that this would ever be the case.
So, what are we solving for? Well, we know Z; we know x1, x2.... xn as our temperatures; and we know y1, y2... yn-1. What we don't know is yn, which is of course the unknown D-value.
Solving for yn, our unknown D-value, yields:
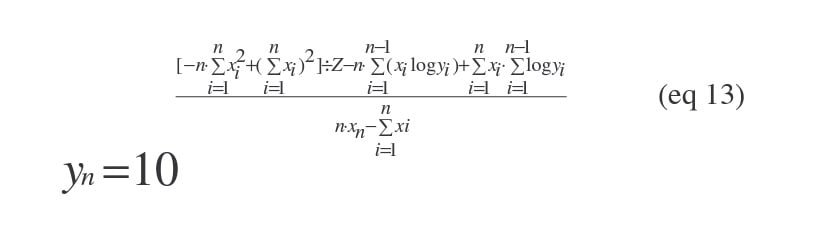
While this equation is somewhat cumbersome, its difficulty can be reduced using the methods of the following example.
Example 2:
Calculate a D-value for 129°C from the following data:
Temperature, D-value
- 115°C, 8.9 minutes
- 121°C, 2.1 minutes
- 124°C, 0.9 minutes
Z-value = 9.5°C
Construct a table to simplify the calculation:
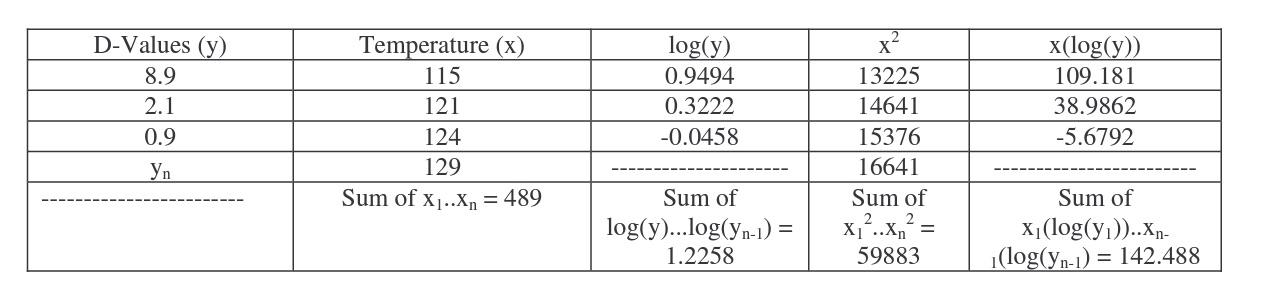
number of x values = n = 4
xn = x4 = 129
Now plug these values into the equation (eq 13).

We can check this value by including it in our data set and calculating a new Z-value. The new Z-value should be the same as the one stated in the problem, 9.5°C.
Can I calculate a D-value using only the data on the certificate?
In most cases a certificate of performance will at least include the D-value at 121°C and the Z-value (where applicable). While it is possible to estimate a D-value from this data, it is not recommended.
Since the Z-value only tells us about the slope of the original regression line and not its y-intercept, the line can exist anywhere along the y-axis. While it will always generate the same Z-value, the D-values it reports will be skewed.
Because we don't know where exactly to place our line, we're simply going to make the assumption that it passes through the D-value at 121°C. Remember that in a perfect world all D-values would exist on our regression line, as they would decrease perfectly exponentially.
For our solution, we're going to use the most basic form for the slope of our line:
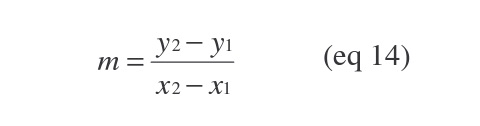
Which in this case will be:
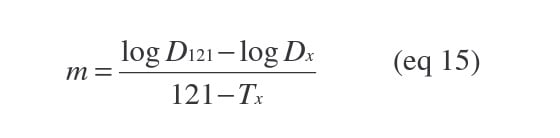
where
- D121 is the D-value at 121°C
- Dx is the unknown D-value
- and Tx is the temperature at which the unknown D-value exists.
Solving for Dx results in:
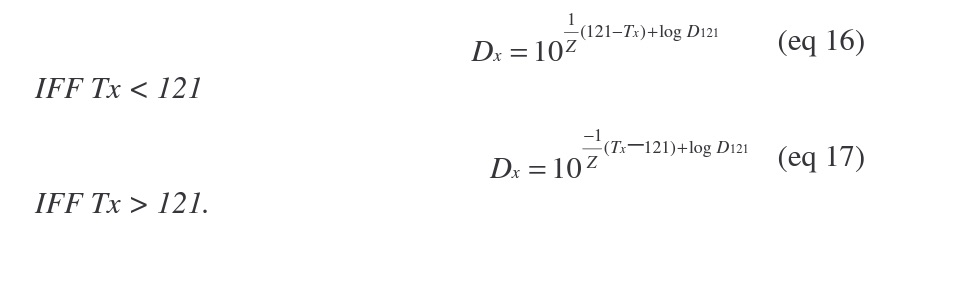
What do the standards say about Z-values?
AAMI, ISO, and EN all discuss Z-values.

What about the USP?
The United States Pharmacopoeia does not discuss Z-values as a performance statistic.
Why are Mesa's standards more strict than EN, ISO, and AAMI?
As every scientist and statistician knows, the more data used in an estimation, the more accurate that estimation will be. We do not feel that using two D-values to determine a Z-value is proper, since the slope of a regression line through only two points will vary greatly from a line through three or more points. Three D-values is the minimum number of points required for practical yet accurate Z-value estimates.
I can't find the Z-value on the certificate that came with the product!?
Z-values are generally only reported for products used in steam and dry heat processes.